아벨 군

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 표기법
3. 성질
4. 분류
5. 예
6. 역사
참조

1. 개요

아벨 군은 군의 일종으로, 군 연산에 대한 교환 법칙이 성립하는 군을 의미한다. 즉, 두 원소의 연산 순서를 바꿔도 결과가 같아야 한다. 아벨 군은 정수환 위의 가군으로 정의할 수도 있으며, 두 정의는 서로 동치이다. 아벨 군의 정의는 결합 법칙, 항등원의 존재, 역원의 존재, 교환 법칙을 만족하는 집합과 연산의 쌍으로 주어진다. 아벨 군은 덧셈 표기법과 곱셈 표기법을 사용하며, 덧셈 표기법에서는 덧셈 항등원을 0, 역원을 마이너스 원으로 표기한다.

아벨 군은 군론, 가군론, 대수기하학, 호몰로지 대수학, 범주론 등 다양한 수학 분야에서 중요한 역할을 한다. 특히, 유한 생성 아벨 군은 완전히 분류되어 있으며, 모든 아벨 유한군은 소수 거듭제곱 차수의 유한 순환군의 직합으로 나타낼 수 있다. 아벨 군의 예시로는 정수의 덧셈군, 순환군, 환, 실수 및 유리수의 덧셈군, 클라인 4원군 등이 있다. 아벨 군이라는 용어는 닐스 헨리크 아벨의 업적을 기리기 위해 명명되었다.

더 읽어볼만한 페이지

닐스 헨리크 아벨 - 아벨상
아벨상은 노르웨이 수학자 닐스 헨리크 아벨을 기려 제정된 수학 분야의 국제적인 상으로, 수학 전반에 걸쳐 뛰어난 업적을 남긴 수학자에게 수여된다.
닐스 헨리크 아벨 - 아벨 범주
아벨 범주는 다양한 수학적 구조를 통합하는 범주론의 중요한 개념으로, 영 대상, 곱과 쌍대곱, 정규 단사 및 전사 사상을 가지며, 완전열, 유도 함자 등을 정의하고, 호몰로지 대수학의 기본 환경을 제공한다.
아벨 군론 - 클라인 4원군
클라인 4원군은 4개의 원소로 이루어진 아벨 군으로, 항등원을 제외한 모든 원소의 차수가 2이며, 유한체 $\mathbb F_4$ 의 덧셈군과 동형이고, 자기 동형군은 3차 대칭군과 동형이며, 다양한 분야에 응용된다.
아벨 군론 - 꼬임 부분군
꼬임 부분군은 아벨 군에서 유한한 차수를 갖는 원소들로 이루어진 부분군이며, 유한 생성 아벨 군의 구조를 이해하는 데 중요한 역할을 하고, 꼬임 부분군은 p-멱 꼬임 부분군들의 직합과 동형이다.

아벨 군
군 이론
분야	수학
유형	대수 구조
이름의 유래	닐스 헨리크 아벨
정의
정의	연산이 교환 법칙을 만족하는 군
다른 이름	가환군
성질
유한 아벨 군의 기본 정리	모든 유한 아벨 군은 순환군의 직접곱으로 표현 가능
군의 크기	소수이면 순환군이고, 따라서 아벨 군임
부분군	아벨 군의 모든 부분군은 정규 부분군임
잉여군	아벨 군의 잉여군은 아벨 군임
유한 생성 아벨 군	유한 생성 아벨 군은 자유 아벨 군과 유한 군의 직접곱으로 표현 가능
관련 항목
관련 개념	군 환 가군
예시	정수 집합 (덧셈 연산) 짝수 정수 집합 (덧셈 연산) 실수 집합 (덧셈 연산) 영이 아닌 실수 집합 (곱셈 연산) 복소수 집합 (덧셈 연산) 영이 아닌 복소수 집합 (곱셈 연산) 순환군 클라인 4군 임의의 벡터 공간 (덧셈 연산) 아벨 군의 직접곱

2. 정의

아벨 군은 교환 법칙이 성립하는 군이다. 즉, 집합 ''G''와 그 위의 이항 연산 "*"가 다음 조건을 만족하면 아벨 군이라고 한다.

# 결합 법칙: ''G''의 임의의 원소 ''a'', ''b'', ''c''에 대해, $a * (b * c) = (a * b) * c$

# 항등원의 존재: ''G''의 어떤 원소 1이 존재하여, ''G''의 임의의 원소 ''a''에 대해 $a * 1 = 1 * a = a$

# 역원의 존재: ''G''의 임의의 원소 ''a''에 대해, 어떤 원소 $a^{-1}$ 이 존재하여, $a * a^{-1} = a^{-1} * a = 1$

# 교환 법칙: ''G''의 임의의 원소 ''a'', ''b''에 대해, $a * b = b * a$

이때, 고려하는 연산이 명백할 때는 연산 기호를 생략하고 ''G''를 아벨 군이라고 부르기도 한다.

아벨 군은 정수환 $\mathbb Z$ 위의 가군으로 정의할 수도 있다. 교환 법칙을 만족시키는 군 $(G,+)$ 이 주어졌다면,

: $n\cdot g=\begin{cases}\overbrace{g+g+\cdots+g}^n&n>0\\(-n)\cdot(-g)&n<0\\0&n=0\end{cases}\qquad\forall n\in\mathbb Z,\;g\in G$

와 같이 정수환의 작용을 정의할 수 있다. 반대로, 정수환 위의 가군 $(G,+,n\cdot_{n\in\mathbb Z})$ 이 주어졌다면, 정수환의 작용을 잊으면 $(G,+)$ 는 교환 법칙을 만족시키는 군을 이룬다.

군 연산이 교환 법칙을 만족하지 않으면 "비아벨 군" 또는 "비교환군"이라고 한다.

2. 1. 표기법

아벨 군에는 덧셈 표기법과 곱셈 표기법 두 가지가 주로 사용된다.

표기법	연산	항등원	거듭제곱	역원
덧셈	$x + y$	0	$nx$	$-x$
곱셈	$x \cdot y$ 또는 $xy$	1	$x^n$	$x^{-1}$

일반적으로 곱셈 표기법은 군에 대한 일반적인 표기법이며, 덧셈 표기법은 가군과 환에 대한 일반적인 표기법이다. 덧셈 표기법은 특정 군이 아벨 군임을 강조하기 위해 사용될 수도 있는데, 아벨 군과 비아벨 군이 모두 고려될 때가 이에 해당한다. 주목할 만한 예외로는 연산이 비아벨 군일 때도 덧셈으로 표기되는 준환과 부분 순서 군이 있다.^[3]^[4]

아벨 군에서는 종종 연산자를 "+"로 표기한다. 이때 항등원을 영원이라고 부르며 0 등으로 나타내고, 역원도 -''a''와 같이 음수 기호를 사용하여 '''마이너스 원''' 또는 '''반수'''라고 부르기도 한다. 또한, ''a'' + (-''b'')는 ''a'' - ''b''로 표기되며, ''a''에서 ''b''를 빼는 뺄셈이 정의된다. 이러한 표기법을 '''덧셈적 표기법'''이라고 부르며, 반대로 앞서 언급한 일반적인 군에서 자주 사용되는 표기법을 '''곱셈적 표기법'''이라고 부르기도 한다.

3. 성질

만약 $n$ 이 자연수이고 $x$ 가 덧셈으로 표현된 아벨 군 $G$ 의 원소라면, $nx$ 는 $x + x + \cdots + x$ ( $n$ 개의 항)으로 정의할 수 있고, $(-n)x = -(nx)$ 이다. 이렇게 하면 $G$ 는 환 $\mathbb{Z}$ 위의 가군이 된다. 사실, $\mathbb{Z}$ 위의 가군은 아벨 군과 같다고 볼 수 있다.^[9]

아벨 군(즉, 주 아이디얼 정역 $\mathbb{Z}$ 위의 가군)에 대한 정리는 다른 주 아이디얼 정역 위의 가군에 대한 정리로 일반화할 수 있는 경우가 많다. 예를 들어 유한 생성 아벨 군의 분류는 주 아이디얼 정역 위의 유한 생성 가군에 대한 구조 정리의 특별한 경우이다. 유한 생성 아벨 군의 경우, 이 정리에 따르면 아벨 군은 꼬임군과 자유 아벨 군의 직합으로 분해될 수 있다. 전자는 소수 $p$ 에 대해 $\mathbb{Z}/p^k\mathbb{Z}$ 형태의 유한 군의 직합으로 표현될 수 있고, 후자는 $\mathbb{Z}$ 의 유한 개 복사본의 직합이다.

$f, g: G \to H$ 가 아벨 군 사이의 두 군 준동형 사상이라면, 그들의 합 $f + g$ 는 $(f + g)(x) = f(x) + g(x)$ 로 정의되며, 이 역시 준동형 사상이다. ( $H$ 가 아벨 군이 아니면 성립하지 않는다.) 따라서 $G$ 에서 $H$ 로 가는 모든 군 준동형 사상의 집합 $\text{Hom}(G,H)$ 는 자체로 아벨 군이다.

벡터 공간의 차원과 비슷하게, 모든 아벨 군은 '''계수'''를 갖는다. 이는 군에서 선형 독립적인 원소 집합의 최대 기수로 정의된다.^[10] 유한 아벨 군과 꼬임군(torsion 군)은 계수가 0이며, 계수가 0인 모든 아벨 군은 꼬임군이다. 정수와 유리수는 계수가 1이며, 유리수의 모든 0이 아닌 가법군도 계수가 1이다. 반면, 0이 아닌 유리수의 곱셈군은 무한한 계수를 가지는데, 소수 집합을 기저로 하는 자유 아벨 군이기 때문이다(산술의 기본 정리에서 비롯됨).

군 $G$ 의 중심 $Z(G)$ 는 $G$ 의 모든 원소와 교환하는 원소의 집합이다. 군 $G$ 가 아벨 군인 것은 그 자체가 중심 $Z(G)$ 와 같을 때뿐이다. 군 $G$ 의 중심은 항상 $G$ 의 특성 아벨 부분군이다. 만약 군을 그 중심으로 나눈 몫군 $G/Z(G)$ 이 순환군이면 $G$ 는 아벨 군이다.^[11]

3. 1. 군론적 성질

순환군 ⊊ 아벨 유한군 ⊊ 유한 생성 아벨 군 ⊊ 아벨 군 ⊊ 데데킨트 군 ⊊ 멱영군 ⊊ 가해군 ⊊ 군과 같은 포함 관계가 성립한다. 특히, 모든 아벨 군은 데데킨트 군이므로, 모든 부분군은 정규 부분군이다.

아벨 군의 직접곱은 아벨 군이며, 아벨 군의 부분군은 아벨 군이다. 그러나 아벨 군의 자유곱은 아벨 군이 아니다. 유한 생성 아벨 군의 유한 개의 직합은 유한 생성 아벨 군을 이룬다. 모든 아벨 유한군은 유한 생성 아벨 군이며, 계수가 0이다.

모든 아벨 군

G

에 대하여,

G

의 계수는

G

의 최소 생성 집합의 크기보다 같거나 작고,

G

의 최소 생성 집합의 크기는

G

의 크기보다 같거나 작다.

아벨 군 가운데 단순군인 것은 소수 크기의 순환군

\mathbb Z/p

밖에 없다.^[6] 유한군이 아벨군임을 확인하기 위해, 곱셈표와 유사한 방식으로 케일리 표를 구성할 수 있다. 이 표의

(i, j)

번째 항목은 곱

g_i \cdot g_j

를 포함한다. 이 표가 주 대각선에 대해 대칭일 때, 그 군은 아벨군이다.^[5]

모든 순환군 $G$ 는 아벨군이다.
모든 환은 덧셈 연산에 대해 아벨군이다. 가환환에서 가역 원소는 아벨 곱셈군을 형성한다.
아벨군의 모든 부분군은 정규 부분군이므로, 각 부분군은 몫군을 생성한다. 아벨군의 부분군, 몫군, 그리고 직합은 다시 아벨군이 된다.

3. 2. 가군론적 성질

아벨 군은 정수환 위의 가군이므로, 가군론을 적용할 수 있다. 가군론적 성질들은 아벨 군의 성질에 다음과 같이 대응한다.

가군의 성질	아벨 군의 성질
자유 가군	자유 아벨 군 (정수환이 주 아이디얼 정역이기 때문)
사영 가군	자유 아벨 군 (정수환이 주 아이디얼 정역이기 때문)
평탄 가군	꼬임 없는 아벨 군 (정수환이 데데킨트 정역이기 때문)
꼬임 없는 가군	꼬임 없는 아벨 군 (정수환이 데데킨트 정역이기 때문)
단사 가군	나눗셈군
유한 생성 가군	유한 생성 아벨 군
단순 가군	아벨 단순군 = 소수 크기의 순환군 $\mathbb Z/p$

아벨 군 $G$ 의 (정수환 위의 가군으로서의) 크룰 차원은 다음과 같다.

: $m=\begin{cases}\inf\{n\in\mathbb Z^+\colon nG=0\}\in\mathbb Z^+&\exists n\in\mathbb Z^+\colon nG=0\\0&\nexists n\in\mathbb Z^+\colon nG=0\end{cases}$

라고 하자. 그렇다면 $G$ 의 크룰 차원은 $\mathbb Z/(m)$ 의 크룰 차원과 같다. 즉, $m=0$ 일 경우 $G$ 의 크룰 차원은 1이며, $m=1$ 인 경우 $G$ 의 크룰 차원은 $-\infty$ 이며, 0 또는 1이 아닌 경우 $G$ 의 크룰 차원은 0이다.

아벨 군 $G$ 의 (정수환 위의 가군으로서의) 길이는 그 합성열(composition series^영어)의 최대 길이와 같다. 예를 들어, 아벨 유한군 $\mathbb Z/(n)$ 의 길이는 $n$ 의 소인수 분해가

: $n=\prod_ip_i^{n_i}$

일 때 $\sum_in_i$ 이다. 무한 순환군 $\mathbb Z$ 의 길이는 무한대이다.

정역 $R$ 위의 가군의 계수는 $\operatorname{rank}M=\dim_{\operatorname{Frac}R}M\otimes_R\operatorname{Frac}R)$ 이다. 여기서 $\operatorname{Frac}R$ 는 $R$ 의 분수체를 뜻하며, $\dim_{\operatorname{Frac}R}$ 는 분수체 위의 벡터 공간으로서의 차원이다. 이 경우, 아벨 군의 가군론적 계수는 아벨 군으로서의 계수와 같다.

3. 3. 대수기하학적 성질

아벨 군은 정수환 위의 가군이다. 대수기하학적으로, 정수환의 스펙트럼은 소수 주 아이디얼을 닫힌 점으로 하는 1차원 스킴이다.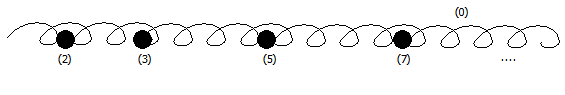

정수환의 그림. 닫힌 점들은 소수로 생성되는 주 아이디얼이며, 이 밖에 일반점 (0)이 있다.

가환환 위의 가군은 가환환의 스펙트럼 위의 가군층을 이룬다. 즉, 아벨 군은 정수환의 스펙트럼

\operatorname{Spec}\mathbb Z

위의 층으로 생각할 수 있다. 이 경우, 유한 생성 아벨 군

:

G=\bigoplus_{\mathfrak p\in\operatorname{Spec}\mathbb Z}\sum_{k=1}^\infty(\mathbb Z/\mathfrak p^k)^{\oplus n(\mathfrak p^k)}

의 지지 집합은

:

\{\mathfrak p\in\operatorname{Spec}\mathbb Z\colon\exists k\colon n(\mathfrak p^k)\ne0\}

이다. 가군층의 직합 및 텐서곱은 아벨 군의 직합 및 텐서곱과 같다. 아벨 군

G

의, 닫힌 점

(p)

위에서의 가군층의 올은 유한체

\mathbb F_p

위의 벡터 공간

:

G\otimes_{\mathbb Z}\mathbb F_p\cong\mathbb F_p^{\oplus(n(0)+\sum_kn(p^k))}

이며, 일반점

(0)

위에서의 가군층의 올은 유리수 위의 벡터 공간

:

G\otimes_{\mathbb Z}\mathbb Q\cong\mathbb Q^{\oplus n(0)}

이다. 즉, 일반점 위에서의 가군층의 차원은 아벨 군의 계수와 같다.

예를 들어, 순환군

\mathbb Z/m

의 지지 집합은

m

의 소인수들이다. 만약

\mathbb Z/m

및

\mathbb Z/n

이 주어졌을 때, 두 아벨 군의 텐서곱은

:

\mathbb Z/\gcd\{m,n\}

이 된다. 특히,

m

과

n

이 서로소라면 이는 자명군이 된다. 기하학적으로, 이는

\mathbb Z/m\otimes\mathbb Z/n

의 지지 집합은

\mathbb Z/m

의 지지 집합과

\mathbb Z/n

의 지지 집합의 교집합이 되기 때문이다. 두 지지 집합이 겹치지 않는다면, 텐서곱이 항상 0이 된다.

3. 4. 호몰로지 대수학적 성질

아벨 군은 정수환 위의 가군으로 간주할 수 있다. 이때 사영 가군은 자유 아벨 군이며, 단사 가군은 나눗셈군이다.

임의의 아벨 군

G

는 자유 아벨 군

F

의 몫군

F/N

으로 나타낼 수 있다.

:

0\to N\to F\to G\to0

자유 아벨 군의 모든 부분군은 자유 아벨 군이므로, 이는 길이가 1인 사영 분해를 이룬다. 따라서, 아벨 군

G

의 사영 차원은 다음과 같다.

$G$ 가 자유 아벨 군일 경우, $\operatorname{pd}_{\mathbb Z}G=0$
$G$ 가 자유 아벨 군이 아닐 경우, $\operatorname{pd}_{\mathbb Z}G=1$

마찬가지로, 임의의 아벨 군

G

은 어떤 나눗셈군

D

의 부분군으로 나타낼 수 있다.

:

0\to G\to D\to Q

나눗셈군의 몫군은 역시 나눗셈군이므로, 이는 길이가 1인 단사 분해를 이룬다. 따라서, 아벨 군

G

의 단사 차원은 다음과 같다.

$G$ 가 나눗셈군일 경우, $\operatorname{id}_{\mathbb Z}G=0$
$G$ 가 나눗셈군이 아닐 경우, $\operatorname{id}_{\mathbb Z}G=1$

3. 5. 범주론적 성질

아벨 군과 군 준동형의 범주

\operatorname{Ab}

는 아벨 범주이며, 다음 성질들이 성립한다.

두 아벨 군 사이의 군 준동형들의 집합은 자연스럽게 아벨 군의 구조를 갖는다. 구체적으로, $\phi,\chi\colon G\to H$ 가 주어졌다면 $(\phi+\chi)\colon g\mapsto \phi(g)+\chi(g)$ 와 같이 정의한다.
모든 유한 곱과 유한 쌍대곱이 존재하며, 서로 같다. 이는 직접곱(=아벨 군의 직합)이다.
분할 보조정리가 성립한다.

폰트랴긴 쌍대성에 의하여, 아벨 군의 범주의 반대 범주는 콤팩트 하우스도르프 아벨 위상군과 연속 군 준동형의 범주와 동치이다.

:

\operatorname{Ab}^{\operatorname{op}}\simeq\operatorname{HausCompAb}

아벨 군과 군 준동형의 범주

\operatorname{Ab}

는 대수 구조 다양체의 범주이므로, 완비 범주이자 쌍대 완비 범주이다. 이 경우, 각종 극한과 쌍대극한은 다음과 같다.

범주론의 개념	아벨 군론의 개념
영 대상	자명군 $0$
곱	군의 직접곱 $\textstyle\prod_{i\in I}G_i$
쌍대곱	아벨 군의 직합 $\textstyle\bigoplus_{i\in I}G_i$
동등자	집합과 함수의 범주에서의 동등자
쌍대동등자	$\phi,\chi\colon G\to H$ 의 쌍대동등자는 $\{\phi(g)-\chi(g)\colon g\in G\}$ 으로부터 생성되는 부분군에 대한 몫군
단사 사상	단사 함수인 군 준동형
전사 사상	전사 함수인 군 준동형
군 대상	아벨 군
단사 대상	나눗셈군
사영 대상	자유 아벨 군

다시 말해, 정수환 위의 단사 가군은 나눗셈군이며, 정수환 위의 사영 가군은 자유 아벨 군이다.

3. 6. 생성 집합, 계수, 높이

아벨 군

G

의 '''생성 집합'''(生成集合, generating set^영어)

S\subset G

는 다음 조건을 만족시키는 부분 집합이다.

임의의 $g\in G$ 에 대하여, 다음 두 조건을 만족시키는 함수 $n\colon S\to\mathbb Z$ 가 존재한다.
$\{s\in S\colon n(s)\ne0\}$ 은 유한 집합이다.
$g=\sum_{s\in S}n(s)s$ 이다.

G

의 '''최소 생성 집합'''(最小生成集合, minimal generating set^영어)은 생성 집합 가운데, 집합의 크기가 가장 작은 것이다. 최소 생성 집합이 유한 집합인 아벨 군을 '''유한 생성 아벨 군'''(有限生成Abel群, finitely generated abelian group^영어)이라고 한다.

아벨 군

G

의 '''일차 독립 부분 집합'''(一次獨立部分集合, linearly independent subset^영어)

A=\{a_i\}_{i\in I}\subset G

는 그 합이 0인 선형 결합이 자명한 선형 결합밖에 없는 부분 집합이다. 즉,

n=(n_i)_{i\in I}

가 유한 개의 성분들만 0이 아닌

|I|

개 음이 아닌 정수들의 순서쌍이라고 하면,

:

\sum_{i\in I}n_ia_i=0

일 필요충분조건은

n=0

인 경우다.

아벨 군

G

의 '''계수'''(階數, rank^영어)

\operatorname{rank}G

는 다음과 같이 두 가지 방법으로 정의될 수 있는 기수이다.

$\operatorname{rank}G$ 는 $G$ 의 일차 독립 부분 집합들의 집합의 크기들의 최댓값이다.
$\operatorname{rank}G=\dim_{\mathbb Q}G\otimes\mathbb Q$ 이다. 여기서 $\otimes$ 는 아벨 군의 텐서곱이다.

따라서, 유리수 위의 벡터 공간의 경우, 아벨 군으로서의 계수는 유리수 위의 벡터 공간으로서의 차원과 같다.

아벨 군

G

의 원소

g\in G

및 소수

p

가 주어졌을 때,

g

의 '''

p

-높이'''(

p

-height^영어)

\operatorname{ht}_p(g)\in\mathbb N\cup\{\infty\}

는 다음과 같다.

:

\operatorname{ht}_p(g)=\sup\{n\in\mathbb N\colon\exists h\in G\colon p^nh=g\}\in\mathbb N\cup\{\infty\}

4. 분류

일반적인 아벨 군은 분류하기 힘들지만, 다음과 같은 부분적인 분류가 존재한다.

유한 생성 아벨 군은 완전히 분류되었다. 즉, 모든 유한 생성 아벨 군은 그 계수 및 꼬임 부분군에 의하여 완전히 분류된다.^[14]
꼬임 부분군이 없는 계수 1의 아벨 군 역시 완전히 분류되었다.^[28]
나눗셈군 역시 완전히 분류되었다.

유한 생성 아벨 군의 경우, 스미스 정규형을 통해 군의 직합 형태로 표현하는 방법을 제공한다.^[14] 이는 정수 행렬을 사용하여 표현이 가능하며, 유한 생성 아벨군 연구가 정수 행렬 연구와 동일함을 의미한다.

가장 단순한 무한 아벨 군은 무한 순환군이다. 유한 생성 아벨 군은 이 무한 순환군의 복사본과 유한 개의 소수 멱수 순환군의 직합으로 분해 가능하다.

하지만, 일반적인 무한 생성 아벨 군의 분류는 완전하지 않다. 가분군과 같이 일부 특수한 형태의 무한 아벨 군만이 완전히 분류되어 있다. 비틀림 군과 비틀림이 없는 군은 무한 아벨 군의 중요한 두 가지 예시이지만, 이들을 조합하는 것만으로는 모든 무한 아벨 군을 설명할 수 없다.

4. 1. 아벨 유한군의 분류

모든 아벨 유한군은 소분해 또는 불변 인자 분해를 통해 유일하게 표현될 수 있다.

'''소분해'''(素分解, prime decomposition^영어):

:

G=\bigoplus_p\bigoplus_{i=1}^{t_p}\mathbb Z/p^{n_{p,i}}\qquad(n_{p,1}\ge n_{p,2}\ge\cdots\ge n_{p,t_p})

:여기서

p

는 소수이다.

'''불변 인자 분해'''(不變因子分解, invariant factor decomposition^영어):

:

\mathbb Z/k_1 \oplus \cdots \oplus \mathbb Z/k_u

:여기서

k_u \mid k_{u-1} \mid \cdots \mid k_1

이다 (

a\mid b

는

a

가

b

의 약수임을 뜻한다).

이 두 분해는 중국인의 나머지 정리를 사용하여 서로 동치임을 보일 수 있다.^[26] 구체적으로,

:

k_1=\prod_pp^{n_{p,1}}

:

k_2=\prod_pp^{n_{p,2}}

:

\vdots

와 같다. 여기서, 만약

i>t_p

라면

n_{p,i}=0

으로 정의한다.

아벨 유한군의 자기 동형군의 크기는 소분해를 이용하여 계산할 수 있다.^[27] 소분해가 주어진 아벨

p

-유한군의 자기 동형군의 크기는 다음과 같다.

:

\left|\operatorname{Aut}\left(\bigoplus_{i=1}^t\mathbb Z/p^{n_i}\right)\right|= \prod_{k=1}^t(p^{t+1-D_k}-p^{k-1})\prod_{j=1}^tp^{n_j(D_j-1)}\prod_{i=1}^tp^{C_i(n_i-1)}

여기서 항상

:

n_1\ge n_2\ge\cdots\ge n_t

이며,

:

C_i=\max\{j\colon n_{p,i}=n_{p,j}\}

:

D_i=\min\{j\colon n_{p,i}=n_{p,j}\}

이다. 임의의 아벨 유한군

:

G=\bigoplus_pG_p

의 자기 동형군은

:

\operatorname{Aut}(G)=\prod_p\operatorname{Aut}(G_p)

이다.

4. 2. 꼬임 부분군이 없는 계수 1 아벨 군의 분류

꼬임 부분군이 자명군이며, 계수가 1인 아벨 군들은 형(type)이라는 개념을 통해 완전히 분류된다.^[28]

계수가 1인 아벨 군

G

가 주어졌다고 하자.

g\in G

(

g\ne0

)에 대하여, 모든 소수

p

에 대한

p

-높이들의 수열

:

\operatorname{ht}(g)=(\operatorname{ht}_2(g),\operatorname{ht}_3(g),\operatorname{ht}_5(g),\dots,\operatorname{ht}_p(g),\dots,)

을 정의할 수 있다. 임의의 두 원소

g,h\in G

(

g\ne 0\ne h

)에 대하여, 계수가 1이므로 항상

:

mg=nh

인

m,n\in\mathbb Z\setminus\{0\}

이 존재한다 (

\gcd(g,h)=1

). 따라서, 만약

p

가

m

또는

n

의 소인수가 아니라면,

\operatorname{ht}_p(g)=\operatorname{ht}_p(h)

가 된다. 즉,

\operatorname{ht}(g)

와

\operatorname{ht}(h)

는 유한 개의 성분을 제외하고는 서로 일치한다. 이러한 두

s,t

에 대하여

:

s\sim t\iff|\{p\colon s_p\ne t_p\}|<\aleph_0

와 같이 동치 관계를 정의하면, 동치류

[\operatorname{ht}(g)]

는

g\in G

에 상관없이 유일하게 정의된다. 이를

G

의 '''형'''(type^영어)

T(G)

라고 하자.

꼬임 부분군이 없는 계수 1의 두 아벨 군

G

,

H

에 대하여 다음 두 조건은 서로 동치이다.

$G$ 와 $H$ 는 서로 동형이다.
두 군은 같은 형을 갖는다. 즉, $T(G)=T(H)$ 이다.

4. 3. 고차 계수 아벨 군

계수가 2 이상인 아벨 군의 분류는 사실상 불가능한 것으로 생각된다. 계수가 2 이상인, 꼬임 부분군이 자명한 아벨 군의 분류는 계수 1인 경우와 비교할 때 (어떤 집합론적인 엄밀한 의미에서) 훨씬 더 어렵다.^[29]

5. 예

기호	설명	계수	최소 생성 집합의 크기	집합의 크기
$\mathbb Z/n$	순환군	0	1	$n$
$\mathbb Z/2\times\mathbb Z/2$	클라인 4원군	0	2	4
$\mathbb Z$	무한 순환군	1	1	$\aleph_0$
$\mathbb Q$	유리수의 덧셈군	1	$\aleph_0$	$\aleph_0$
$\mathbb Q^n$	유클리드 공간의 유리점	$n$	$\aleph_0$	$\aleph_0$
$\mathbb Q^+\cong\bigoplus_p\mathbb Z$	양의 유리수의 곱셈군(=가산 개의 생성원의 자유 아벨 군)	$\aleph_0$	$\aleph_0$	$\aleph_0$
$(\mathbb Z/2)^{\oplus\aleph_0}$	2차 순환군의 가산 무한 직합	0	$\aleph_0$	$\aleph_0$
$\mathbb R$	실수의 덧셈군	$2^{\aleph_0}$	$2^{\aleph_0}$	$2^{\aleph_0}$
$\mathbb R^n$	유클리드 공간	$2^{\aleph_0}$	$2^{\aleph_0}$	$2^{\aleph_0}$

정수와 덧셈 연산 $+$ 에 대해, $(\mathbb{Z}, +)$ 로 표기되는 경우, 덧셈은 교환법칙이 성립하므로 아벨군이다.
모든 순환군 $G$ 는 아벨군이다. 예를 들어 정수 $\mathbb{Z}$ 와 정수 모듈로 $n$ $\mathbb{Z}/n \mathbb{Z}$ 는 아벨군을 이룬다.
모든 환은 덧셈 연산에 대해 아벨군이다. 가환환의 단위는 아벨 곱셈군을 형성한다. 특히, 실수는 덧셈에 대해 아벨군을 이루며, 0이 아닌 실수는 곱셈에 대해 아벨군을 이룬다.
정수 전체 '''Z''', 유리수 전체 '''Q''', 실수 전체 '''R''', 복소수 전체 '''C'''는 모두 일반적인 덧셈에 관해 아벨 군이다.
0을 제외한 유리수 집합 '''Q'''^*, 0을 제외한 실수 집합 '''R'''^*, 0을 제외한 복소수 집합 '''C'''^*는 곱셈에 관해 아벨 군이 된다.
타원 곡선 ''y''² = ''x''³ + ''ax'' + ''b''의 해 집합에는 덧셈을 정의할 수 있으며, 아벨 군이 된다.

6. 역사

군론은 고차 방정식의 해법 가능성 여부에 대한 갈루아 이론으로부터 출발하였다. 이를 연구하던 닐스 헨리크 아벨은 어떤 다항식의 분해체의 갈루아 군이 아벨 군일 경우, 다항식의 해를 거듭제곱근만으로 나타낼 수 있음을 보였다.^[7]^[8]

카미유 조르당은 노르웨이 출신의 수학자 닐스 헨리크 아벨의 이름을 따서 아벨 군이라 명명했는데, 이는 아벨이 다항식의 군의 가환성이 다항식의 근을 근을 사용하여 계산할 수 있음을 발견했기 때문이다.^[7]^[8]

참조

_[1] Harvard citation
_[2] 서적 Pairwise Comparisons Method: Theory and Applications in Decision Making https://books.google[...] Springer Nature Switzerland
_[3] 서적 Groups, Rings, Modules https://books.google[...] Dover Publications
_[4] 서적 Intense Automorphisms of Finite Groups https://books.google[...] American Mathematical Society
_[5] 서적 Theory of Groups and Symmetries: Finite Groups, Lie Groups, and Lie Algebras https://books.google[...] World Scientific
_[6] 서적 https://books.google[...]
_[7] 서적 Galois Theory https://books.google[...] John Wiley & Sons
_[8] 서적 Mathematics of Big Data https://google.com/b[...] MIT Press
_[9] 서적 'Abelian Groups and Modules: International Conference in Dublin, August 10–14, 1998' https://books.google[...] Springer Basel AG
_[10] 서적 'Linear Groups: The Accent on Infinite Dimensionality' https://books.google[...] Taylor & Francis
_[11] 서적 https://books.google[...]
_[12] 서적 https://books.google[...]
_[13] 서적 'The Theory of Finite Groups: An Introduction' https://books.google[...] Springer Verlag
_[14] 서적 'Groups and Computation II: Workshop on Groups and Computation, June 7–10, 1995' https://books.google[...] AMS
_[15] 문서
_[16] 문서
_[17] 서적 Rings and Things and a Fine Array of Twentieth Century Associative Algebra https://books.google[...] AMS
_[18] 서적 Invariant Descriptive Set Theory https://google.com/b[...] CRC Press
_[19] 서적 "Products of Slender Abelian Groups", in Göbel, R., & Walker, E., eds., ''Abelian Group Theory: Proceedings of the Third Conference Held on Abelian Group Theory at Oberwolfach, August 11-17, 1985'' https://books.google[...] Gordon & Breach
_[20] 서적 'Algebra 2: Linear Algebra, Galois Theory, Representation Theory, Group Extensions and Schur Multiplier' https://books.google[...] Springer
_[21] 웹사이트 Abel Prize Awarded: The Mathematicians' Nobel https://web.archive.[...] 2016-07-03
_[22] 웹사이트 Abel Prize Awarded: The Mathematicians' Nobel http://www.maa.org/d[...] 2016-07-03
_[23] 서적 Galois Theory Wiley-Interscience 2004
_[24] 서적
_[25] 서적
_[26] 서적 Algebra Springer 1989
_[27] 저널 Automorphisms of finite Abelian groups https://archive.org/[...] 2007-12
_[28] 서적 Infinite Abelian group theory https://archive.org/[...] University of Chicago Press 1970
_[29] 저널 The classification problem for torsion-free abelian groups of finite rank 2003-01

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com